Application
The reactance chart, sometimes called an impedance chart, is a very useful design tool for power supply design and other electronic and electrical engineering applications. With the reactance chart, the practicing engineer can quickly find the following items:
- impedance values of capacitors and inductors at specified frequencies,
- required values of capacitors, inductors, and resistors for various applications,
- impedance asymptotes of various networks of capacitors, inductances, and resistances,
- asymptotes of network transfer functions,
- circuit resonance frequencies,
- resonance Q-factor,
- many other items.
Unlike other numerical analysis tools which depend upon computer computation, the reactance chart created by hand has the advantage in that the user is creating asymptotic plots which lend intuitive understanding to the circuit under consideration. Pole and zero locations, and the effects of component values are easily seen. In contrast, when using computer created Bode plots, the poles and zero locations are often not easily seen.
Chart Explanation
For your reference and convenience, please download a free .pdf version of a reactance chart optimized for the power supply designer for charting by hand sketching. Reactance charting can also be done with software drawing tools such as Microsoft Visio. If you are skilled with Visio, download a Visio version of the reactance chart. In addition to the chart itself, this version of the reactance chart also contains extra space for documentation at the top and extra space for designer notes at the bottom. If using the .pdf version for hand sketching, I recommend laminating the reactance chart and making multi-color plots with Sharpie fine point markers. Multi-color Sharpie marker packages are available at office supply stores such as Staples. When you want to re-use the chart, erase the old marks with isopropyl alcohol 91% which is cheaply available at drug stores such as Walgreens. The basic reactance chart has logarithmic scales for frequency, resistance, capacitance, and inductance. The frequency scale is along the x-axis. The resistance scale is along the y-axis. The inductance scale is shown as diagonal lines with values of inductance increasing as frequency is increased. The capacitance scale is shown as diagonal lines with values of capacitance decreasing as frequency is increased. The inductance and capacitance scales obey the formulas for inductive reactance and capacitive reactance vs. frequency:
Inductive Reactance = 2*pi*frequency*inductance
Capacitive Reactance = 1/(2*pi*frequency*capacitance)
Inductive reactance and capacitive reactance are read on the same scale as resistance. Reactance charts can also come with additional scales. One of the most useful for power supply design is an additional y-axis scale for gain which can be shown in decibel and non-decibels. When drawing the combination reactance of two elements in series, just use the higher impedance as an approximation. Conversely, when drawing the combination impedance of two elements in parallel, just use the lower impedance as an approximation.
Exercise
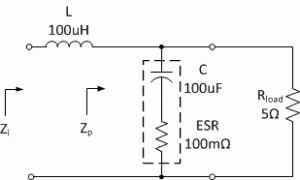
Let’s graphically develop the transfer function of an LC low pass filter with a load resistance as an exercise. We will use a capacitor with significant ESR (Equivalent Series Resistance). My solution to this tutorial exercise is found at Reactance Chart, LC Low Pass Filter Transfer Function. This is the filter schematic:
The transfer function, by the voltage divider relationship is the parallel impedance of the capacitor and the load resistor, Zp, divided by the total input impedance, Zi: H(s) = Zp/Zi We will first plot the asymptotes of the parallel impedance of the capacitor and load resistor, Zp, as follows:
- Since the load resistor is in parallel with the capacitor, the load resistor will dominate the output impedance at low frequencies. Put a mark on the left axis of the reactance chart corresponding to 5 ohms.
- The ESR of the capacitor will dominate the output impedance at high frequencies. Put a mark on the right axis at 100 milliohms.
- In the mid frequency range, the impedance is dominated by the capacitor. Draw a diagonal line along 100uF beginning at 5 ohms and ending at 100 milliohms.
- Complete the horizontal lines representing the load resistance and the ESR.
- Label the different parts of the plot to show which component is dominating each part.
This operation should result in a three part line beginning at 5 ohms at low frequency up to about 159Hz, then following the 100uF line to 100 milliohms at about 15.9kHz, then following the 100 milliohm line to high frequency. This plot represents, Zp, and is shown in blue in my solution. An extension of the ESR is shown in orange for later use in evaluating the Q-factor. Next, draw the asymptotes for the input impedance, Zi, with load as follows:
- First put a mark for 100uH at the high frequency end of the chart to represent the inductive reactance.
- Note that the inductor is in series with the parallel impedance of the output capacitor and load resistance, Zp, so we select the higher of the two impedances as the input impedance. Therefore draw a segmented line along the asymptotes of parallel impedance of the capacitor and load resistor, Zp, at low frequencies up to where the inductive reactance plot would intersect with the plot of parallel combination of capacitor impedance and load resistance, Zp.
- At higher frequencies, as determined by the point at which the two plots intersect, the input impedance is dominated by the inductor. Therefore draw the plot so that it follows the inductive reactance plot.
- Label the different parts of the plot to show which component is dominating each part.
My solution for Zi is shown in green. Note that the frequency at which the inductive reactance asymptote intersects with the parallel impedance of the output capacitor and load resistance, Zp, is a resonant frequency since the inductive reactance and capacitive reactance are equal in magnitude but opposite in sign resulting in impedance cancellation. To get the transfer function, we graphically divide the parallel impedance of the output capacitor and load resistance, Zp, by the input impedance, Zi. Plot the result for the entire curve. My solution for the transfer function is shown in red. Asymptote wise, the result is a gain of one (unity gain) up to the resonant frequency of 1.59kHz. At the resonant frequency, there is a resonant double pole, and the transfer function begins a rolloff at a -2 slope (-40dB per decade). At 15.9kHz, the slope changes to -1 (-20dB per decade) due to the zero created by the ESR and the capacitance. At the resonant frequency, I prefer to illustrate the resonance as a simple impulse with magnitude equal to the Q-factor. The resonance Q-factor can be determined by dividing the characteristic impedance (the impedance in ohms at the resonant frequency of either the inductor or the capacitor) by the ESR. The ESR limits the resonance in this case. It is found that the Q-factor is 10 (20dB). After plotting the gain, we should be able to see graphically where breakpoints are. I prefer to circle them to make them stand out clearly. By inspecting the impedance plots used to generate the gain plot, we should be able to see which components are controlling the gain plot characteristics. The following graphic is my solution for this exercise: Reactance Chart, LC Low Pass Filter Transfer Function This is the end of this tutorial about reactance charts.
If you need assistance with power electronics design, call or email us today for help with your requirements. You can also go to our power electronics consultant website for more information about our services for business clients. Thank you for reading this tutorial article entitled “Reactance Chart Tutorial”